原文作者:Scroll 研究員Andy Arditi
編譯: DeFi 之道
感謝Yi Sun 和Kobi Gurkan 的反饋和評論。

圖片來源:由無界版圖AI工俱生成
簡介
由於數學複雜性,零知識證明在其周圍形成了一種神秘的氣質,它們被親切地稱為“月球數學”,因為它們被大多數人視為超凡脫俗的魔法。
我們Scroll 想要揭開零知識證明內部運作的神秘面紗,這並沒有讓它們變得不那麼神奇,但我們認為幫助社區了解這些技術是很重要的。
在這篇文章中,我們介紹了很多零知識證明系統的關鍵要素:多項式承諾(polynomial commitment)方案。然後我們簡要解釋一下KZG,它是實踐中使用最廣泛的多項式承諾方案之一。接著,我們會繼續討論如何在Scroll 的zk-rollups 以及以太坊的Proto-Danksharding 中使用KZG。最後,我們展示了zk-rollups 以及Proto-Danksharding 如何能夠高效、優雅地相互集成——這種集成是通過它們各自使用多項式承諾方案來實現的。
為什麼我們要討論多項式?
多項式是非常強大的工具,它們在很多不同領域都有有用的應用。多項式可用於以一種有效的方式表示大型對象。
我們可以表示為多項式的一個標準對像是域元素
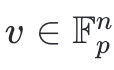
的n 維向量。我們可以製作一個多項式ϕ(x) ,通過確保ϕ(x) 通過點(i,vi)(i=1,2,…,n)來表示v。
例如,我們可以取3 維向量v=[2,0,6],並將其表示為多項式ϕ(x)=4x^2−14x+12. 你可以插入值來驗證ϕ(1)=2, ϕ(2) = 0 ,以及ϕ(3)=6。這樣,多項式ϕ(x) “編碼”了向量v。
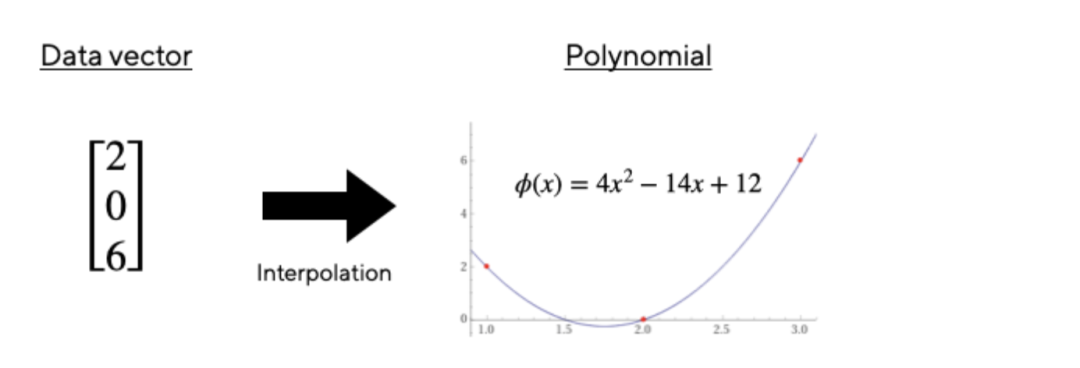
總的來說,取n 個任意點,並找到一個唯一的n-1 次多項式(它通過所有這些點)是可能的。這個過程被稱為“多項式插值”,並且有人已建立了有效完成這個任務的方法。 (查看Wolfram Alpha 提供的這個漂亮的在線工具,它可以在給定輸入向量的情況下插值多項式!)
什麼是多項式承諾(polynomial commitment)方案?為什麼它們是有用的?
多項式承諾方案是具有一些不錯的附加屬性的承諾方案。在一般的承諾方案中,committer 通過輸出一些commitment c 來承諾一則消息m。 committer 隨後可以顯示消息m,驗證者可以驗證commitment c 確實對應於m。承諾方案應該是“綁定的”(一旦發布c,committer 應該無法找到其他一些消息,即發布c 不應洩露有關底層消息m 的任何信息)。
現在,使用多項式承諾方案,committer 提交一個多項式ϕ,而不是一些任意消息m。多項式承諾方案滿足上述正常承諾方案的屬性,並且還實現了一個附加屬性:committer 應該能夠“開放”對承諾多項式的某些評估,而不會透露整個事情。例如,committer 應該能夠證明ϕ(a)=b 而無需確切透露ϕ(x) 是什麼。
這是一個非常棒的屬性,它對於零知識應用是非常有用的!我們可用它來證明我們有一些滿足某些性質的多項式(在這種情況下,它通過某個點(a,b)),而無需揭示多項式是什麼!
這個屬性有用的另一個原因是,commitment c 通常比它所代表的多項式要小得多。我們將看到一個承諾方案,其中任意大次數的多項式可以通過其commitment 表示為單個組元素。當考慮在鏈上發布數據時,這尤為可取,因為區塊空間是一種寶貴的資產,任何形式的壓縮都可立即轉化為成本上的節約。
KZG 多項式承諾方案
好的,現在我們已經簡單了解了多項式承諾方案,讓我們看看如何實際構建一個。我們將關注的是一個稱為Kate-Zaverucha-Goldberg (簡稱KZG) 多項式承諾方案。 KZG 被廣泛用於區塊鏈領域的許多任務(它已經被Scroll 的證明系統使用,並且很快將通過Proto-Danksharding (EIP-4844) 集成到以太坊的協議中)。稍後我們將詳細介紹這些用例中的每一個。
本節將簡要概述KZG 多項式承諾方案的數學結構,它並不是全面的,但應該能清楚地說明事情是如何運作的。對於數學愛好者,我們將在本節末尾提供一些進一步的參考資料。
無論如何,讓我們從解釋開始。 KZG 多項式承諾方案由四個步驟組成:
步驟1(設置):
1、第一步是一次性可信設置。完成此步驟後,可以重複其他步驟以提交和揭示各種不同的多項式。
2、設g為一些配對友好的橢圓曲線群
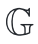
的生成器。
3、設l為我們要承諾的多項式的最大次數。
4、選擇一些隨機field 元素
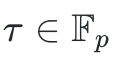
5、計算
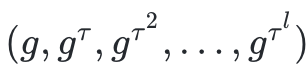
,然後將其公開發布(注意τ 不應該被揭示,它是設置的一個秘密參數,應該在設置儀式後丟棄它,這樣沒有人可以弄清楚它的值)
步驟2 (Commit to多項式):
1、給定一個多項式
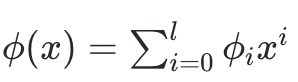
2、計算並輸出commitment

儘管committer 不能直接計算
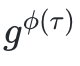
,因為他並不知道τ,他可以使用設置
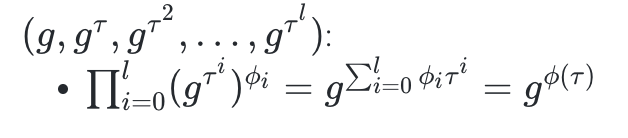
的輸出計算它。
步驟3 (證明一個評估):
1、給定一個評估ϕ(a)=b
2、計算並輸出證明
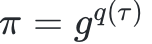
其中
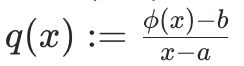
,這被稱為“商多項式”。請注意,當且僅當φ(a)=b 時,這樣的q(x) 才存在。因此,該商多項式的存在可作為評估的證明。
步驟4 (驗證一個評估證明):
1、給定一個commitment
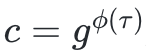
,一個評估ϕ(a)=b,以及一個證明
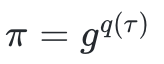
2、驗證
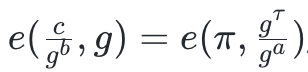
,其中e 是一個non-trivial 雙線性映射。
一些代數(見下面的鏈接註釋)表明這相當於檢查步驟3 中的屬性在τ
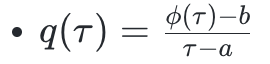
時是否成立。
雙線性映射使我們能夠在不知道秘密設置參數τ 的情況下檢查此屬性。
一旦驗證完成,我們可以得出商多項式是正確的結論(概率極高),因此評估是正確的。
這是KZG 背後數學的一個非常簡化的講解,其中省略了一些細節。要了解更多深度的東西(並查看一個很酷的擴展,你可以使用一個證明來證明多個評估),請查看以下的優秀資源:
1、Dankrad Feist 的KZG 筆記;
2、Alin Tomescu 的KZG 筆記;
KZG 多項式commitment 方案的用例
1、Scroll 的zk-rollups
在zk-rollups 的情況下,我們想證明發生在L2 上的一些計算是有效的。簡單來講,發生在L2 上的計算可通過稱為“ witness 生成”的過程表示為二維矩陣。然後可以用多項式列表來表示矩陣- 每列都可以編碼為其自己的一維向量。然後,計算的有效性可以表示為這些多項式之間必須保持的一組數學關係。 [2] 例如,如果前三列分別由多項式a(x)、b(x) 以及c(x) 表示,我們可能需要關係a(x)⋅b(x)−c(x)=0 保持。多項式(代表計算)是否滿足這些“正確性約束”可通過在一些隨機點評估多項式來確定。如果“正確性約束”在這些隨機點上得到了具體的滿足,則一名驗證者可以非常高的概率斷言計算是正確的。 [3]
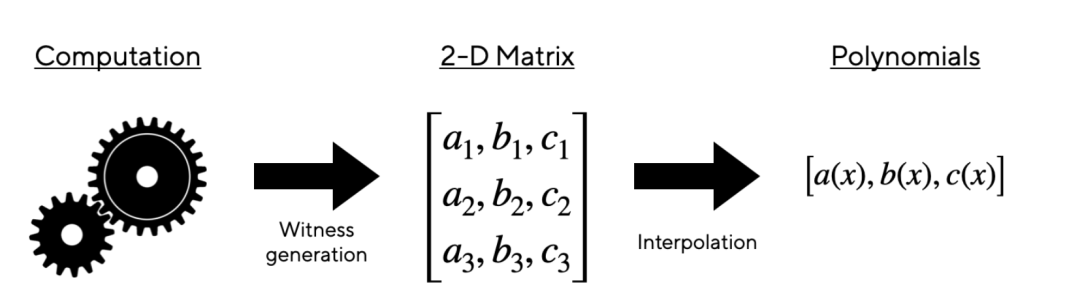
人們可以很自然地看到像KZG 這樣的多項式承諾方案,是如何直接插入到這個範式中的:rollup 將commit to 一組多項式,它們一起代表計算。然後,驗證者可要求對一些隨機點進行評估,以檢查正確性約束是否成立,從而驗證多項式表示的計算是否有效。 [4]
Scroll 專門將KZG 用於其多項式承諾方案。還有一些其他的承諾方案也可以發揮類似的作用,但與KZG 相比,它們目前都有缺點:
1、Inner Product Argument (IPA)方案很有吸引力,因為它不需要可信設置,並且還能以有效的方式遞歸組合。但是,它需要一個特定的橢圓曲線循環(稱為“Pasta 曲線”)才能實現其良好的遞歸特性。以太坊目前不支持對這些Pasta 曲線進行有效操作,這意味著在以太坊執行層進行的證明驗證效率極低。如果在沒有遞歸特性的情況下使用(例如,使用非Pasta 曲線),IPA 的證明驗證時間會隨著電路的大小線性增長,這使得它對於zk-rollups 所需的巨大電路而言是不可行的。
2、Fast Reed-Solomon IOP of Proximity (FRI)方案也不需要可信設置,它不依賴橢圓曲線密碼學,因此具有快速的證明生成(生成證明不需要昂貴的橢圓曲線操作),並且它是抗量子計算的。但是,與KZG 相比,FRI 方案的證明大小和驗證時間都很大。
2、以太坊的Proto-Danksharding
Proto-Danksharding (EIP-4844) 是一項提案,其旨在降低rollup 在以太坊L1 上發布數據的成本,它將通過引入一種稱為“blob-carrying transaction”的新交易類型來做到這一點。這種新的交易類型將攜帶一個更大的數據blob(大約128 kB)。但是,數據blob 將無法從以太坊的執行層訪問(即智能合約不能直接讀取數據blob)。相反,只有對數據blob 的commitment才能從執行層訪問。
現在,我們應該如何創建對數據blob 的commitment?我們可通過簡單地哈希數據blob 來生成一個commitment。但這存在一點限制,因為我們無法在不揭示整個事物的情況下證明數據blob 的任何屬性。 [5]
我們也可以將數據blob 視為一個多項式(請記住,將諸如數據向量之類的數學對象表示為多項式很容易),然後使用一個多項式承諾方案來提交數據。這使我們不僅能夠實現對數據的commitment,而且能夠有效地檢查數據blob 的某些屬性,而無需讀取整個數據。
多項式承諾方案為數據blob 啟用的一項非常有用的功能,是數據可用性採樣(DAS)。使用DAS,驗證者可以驗證數據blob 的正確性和可用性,而無需下載整個數據blob。我們不會深入解釋DAS 的具體工作原理,但它是由我們上面討論的多項式承諾方案的特殊屬性實現的。雖然DAS 的實際實施並未包含在最初的Proto-Danksharding (EIP 4844) 提案中,但它將在不久之後實施,即以太坊實現“完整” 的Danksharding 時。
以太坊計劃專門使用KZG 作為其多項式承諾方案。研究人員探索了其他多項式承諾方案,並得出結論認為,KZG 在中短期內為以太坊的Danksharding 路線圖帶來了最優雅、最高效的實現。 [6]
3、Scroll 的zk-rollups 和以太坊的Proto-Danksharding 如何實現交互?
我們現在討論了KZG 方案的兩個看似獨立的用途:Scroll 使用它來提交在L2 上執行的計算,而以太坊使用它來提交數據blob。現在我們將看看KZG 的這兩種用途,如何以一種很酷的方式交互在一起!
在L2 上處理一批交易併計算出新的狀態根後,Scroll 將基本上將三件事發佈到以太坊L1:
- T,在L2 上執行的交易列表;
- Si,在time-step i 的新狀態根;
- π,新狀態根Si 為有效的一個證明;
我們不僅要驗證新的狀態根Si 是有效的(即存在一些交易列表,當正確執行時,會導致先前的狀態根Si-1更改為新的狀態根Si),而且交易列表T 實際上是導致狀態根從Si-1 變為Si 的交易列表,為了實現這一點,我們需要以某種方式強制T 和π 之間的連接。
T 將作為數據blob 發布,因此驗證者合約將有權訪問它的KZG commitment。證明π 本身將包含對錶示計算的各種多項式的KZG commitment。一個在π 內提交的多項式是表示已處理交易列表的多項式。因此,我們對相同的數據有兩個單獨的KZG commitment,我們稱它們為CT (來自數據blob)以及Cπ(來自證明),假設它們代表相同的基礎多項式φT (這個多項式是事務列表T 的一個表示)。我們可通過“等價證明”有效地檢查兩個commitment 是否表示相同的多項式:
1、計算
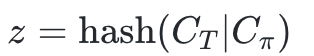
2、在commitment CT 以及Cπ 下發布φ(z)=a 的評估證明
這裡的想法是選擇一個隨機(ish)點,並檢查兩個多項式之間的相等性。如果多項式在隨機選擇的點處相等(並且總點的數量足夠大),則兩個多項式相同的概率非常高。 [7]
這種等價性證明實際上適用於多項式承諾方案的任何組合[8]——如果一個是FRI commitment,而另一個是KZG commitment,這實際並不重要,只要兩者都可以在某個點打開即可。
總結
讓我們回顧一下。
我們從簡單解釋多項式開始,多項式是可以輕鬆表示大型數學對象的有用對象。當我們引入多項式承諾方案時,它們變得更加有用。多項式承諾方案類似於普通的密碼學承諾方案,其具有可以在不揭示整個多項式的情況下證明點評估的附加屬性。
然後,我們對最流行的多項式承諾方案之一KZG 進行了數學描述,該方案有四個步驟:(1)一次性可信設置;(2)一個commitment
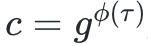
;(3)一個證明
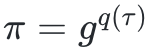
,其中q(x) 是一個商多項式;(4)使用一個雙線性映射進行驗證,檢查ϕ(x) 和q(x) 之間的關係是否正確。
多項式承諾方案的點評估(point-evaluation)特性可以實現非常酷的應用。
我們在zk-rollups 的情況下看到了一個這樣的應用:計算表示為一個多項式,並且可通過檢查多項式是否滿足某些約束來驗證其有效性。由於多項式承諾方案允許點評估證明,zk-rollups 可以簡單地使用簡潔的commitment 來表示計算,而不是冗長的多項式本身。
另一個應用是Proto-Danksharding:數據blob 表示為多項式,它們的commitment 通過KZG 計算。 KZG 的數學特性支持數據可用性採樣(DAS),這對於以太坊數據層的擴容是至關重要的。
最後,我們檢查了Scroll 的zk-rollup 證明中的commitment 如何與以太坊上的數據blob commitment 進行交互。
腳註
1、雖然這聽起來是一項艱鉅的任務,但研究人員已通過使用多方計算(MPC) 建立了以弱信任假設(1-of-N信任假設)進行此類可信設置儀式的方法。有關可信設置如何工作的更多信息,請查看Vitalik 撰寫的這篇文章。
2、這種將計算轉換為數學對象並將其有效性表達為數學關係的過程稱為“算術化”(arithmetization)。有多種方法可以進行這種轉換,而Scroll 使用的是Plonkish 算術化。
3、這個想法被正式稱為Schwartz Zippel 引理,它被廣泛用於有效地驗證多項式的屬性。
4、請注意,驗證者在隨機點查詢多項式的這種交互式挑戰可通過Fiat-Shamir 變換轉換為非交互式協議。
5、我們也可以使用簡潔的證明來證明數據blob 的某些屬性(例如,證明哈希到正確哈希的數據的知識,然後證明該數據的某些屬性),但是這對於每次需要訪問/驗證關於數據blob 的信息執行來說太昂貴了。
6、從長遠來看,KZG 可能需要更換成抗量子的多項式承諾方案。 Proto-Danksharding 的實施方式使得承諾方案可以在未來被替換掉。
7、這再次源自Schwartz Zippel 引理。請注意,在提交數據之前,證明者必須不能知道評估點z 的值,這一點很重要- 這將使證明者能夠輕鬆構建一個偽多項式,該多項式滿足z 處的等式檢查。通過將z 設置為兩個承諾的哈希值,證明者在兩個多項式提交之前無法知道z。
8、然而,當兩個多項式承諾方案在不同的組上運行時,就會出現一個複雜的問題。例如,Scroll 目前使用的是BN254 曲線,而以太坊計劃將BLS12-381 曲線用於Proto Danksharding。在這種情況下,我們無法直接比較組元素,就像上面概述的等價證明一樣。但我們也有一種解決方法,你可以在Dankrad Feist 的筆記中閱讀到。












